Background: In regression models, the posterior distribution on the regression coefficients and intercept can be strongly correlated, causing some MCMC samplers to become inefficient as they "bang into the walls" of the diagonal ridge in parameter space. There are various ways to address this problem, but one simple way is by standardizing the data (or at least subtracting out the mean), and then converting the MCMC-derived parameters back to the original scale of the data. This approach was taken in the book (DBDA) for using BUGS, and continued, vestigially, in the programs that were converted to JAGS even though JAGS is often less susceptible to the problem.
The news in this post is that a reader, Francis Campos, caught an error in the formulas for the translation from standardized data to original-scale data, for the particular case of the multiple linear regression model with
two predictors and a multiplicative interaction. Specifically, part of Equation 17.5, at the top of p.472, has two subscripts reversed, and should be changed as shown in red here:
 |
| Correction to Eqn. 17.5, top of p. 472 |
It turns out that the error was not only in the printed equation. It was also in the programs MultiLinRegressInterBrugs.R and MultiLinRegressInterJags.R, and this error caused the graphical output to be wrong as well. The corrected programs are now available at
the program repository, and the corrected figures are included below. (In a separate program, I verified the new results simply by removing the standardization of the data and the transformation back to original scale. JAGS handles the unstandardized,
original-scale data very efficiently.) Fortunately, nothing conceptual in the discussion in the book needs to be changed. All the conceptual points still apply, even though the graphical details have changed as shown here:
 |
| Top of Fig. 17.9, p. 473, corrected. |
 |
| Bottom of Fig. 17.9, p. 473, corrected. |
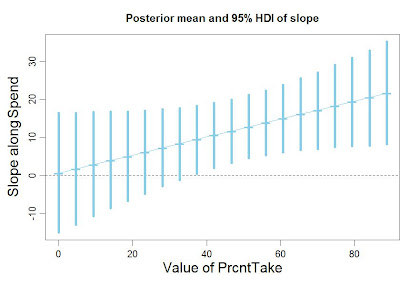 |
| Figure 17.10, p. 474, corrected. |
My thanks to Francis Campos for finding the error and alerting me to it!




Lets say that the regression model is hierarchical with random slopes and intercepts for each subject. Now we center the predictor to speed the MCMC. You show how to back transform the random slopes. Great. But what if we also wanted to back transfers the intercept variances? This requires (I think) a bivariate normal model for subject intercept and slope. We need the covariance to back transform. If I am right it would be good to point this out in the next version of your nice book.
ReplyDeleteDave leblond
I need command for bayesian linear multiple model estimation with (uniform or jeffery) prior in R studio please any one give me help...
ReplyDelete