Bayesian estimation supersedes the t test

New version of May 27, 2012:
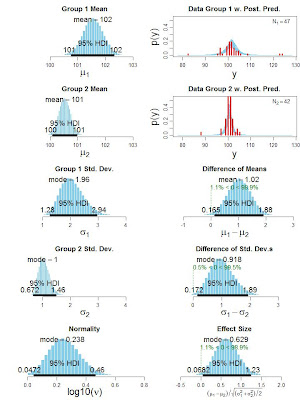
Bayesian estimation for two groups provides complete distributions of credible values for the effect size, group means and their difference, standard deviations and their difference, and the normality of the data. The method handles outliers. The decision rule can accept the null value (unlike traditional t tests) when certainty in the estimate is high (unlike Bayesian model comparison using Bayes factors). The method also yields precise estimates of statistical power for various research goals. The software and programs are free, and run on Macintosh, Linux, and Windows platforms. See this linked page for the latest paper and the software.

Search tag: BEST (for Bayesian estimation)

(This is the second revision of a the first version announced at a previous post.)

Split-Plot Design in JAGS: Revised version

A previous post reported an analysis of a "split plot" design, in which one factor is between subjects and a second factor is within subjects. That program has now been revised, and the advantage of Bayesian analysis over NHST has been confirmed.

My heartfelt thanks to Wolf Vanpaemel for pointing out an error in one of the contrast analyses in the originally posted program. I have now corrected the error and expanded the program to handle the intended contrast. Subsequent discussion with Wolf also prompted me to think harder about whether the model I specified really matched the model used by NHST analyses, and whether the apparent advantage of the Bayesian analysis (reported in the previous post) really made sense. They do, as I explain below. I also revised other aspects of the program to incorporate the improvements in the most recent forms of the other ANOVA-type programs, as reported at this previous post. (By the way, you may recall that Wolf and co-author Francis Tuerlinckx wrote a review of the book.)

A reminder of the split plot design:
Consider an example provided by Maxwell & Delaney (2004, Designing Experiments and Analyzing Data: A Model Comparison Perspective, 2nd Edition, Erlbaum; Ch. 12). (As I've mentioned elsewhere, if you must learn NHST, their book is a great resource.) A perceptual psychologist is studying response times for identifying letters flashed on a screen. The letters can be rotated off of vertical by zero degrees, four degrees, or eight degrees. Every subject responds many times to letters at each of the three angles. The experimenter (for unknown reasons) analyzes only the median response time of each subject at each angle. Thus, each subject contributes only one datum at each level of angle (factor B). There are two types of subjects: "young" and "old." Age of subject is factor A. The structure of the data is shown below. Y is the median response time, in milliseconds. There are 10 subjects per Age group.

Y	Subj	Angle	Age
450	1	B1(Zero)	A1(Young)
510	1	B2(Four)	A1(Young)
630	1	B3(Eight)	A1(Young)
390	2	B1(Zero)	A1(Young)
480	2	B2(Four)	A1(Young)
540	2	B3(Eight)	A1(Young)
...	...	...	...
510	10	B1(Zero)	A1(Young)
540	10	B2(Four)	A1(Young)
660	10	B3(Eight)	A1(Young)
420	11	B1(Zero)	A2(Old)
570	11	B2(Four)	A2(Old)
690	11	B3(Eight)	A2(Old)
600	12	B1(Zero)	A2(Old)
720	12	B2(Four)	A2(Old)
810	12	B3(Eight)	A2(Old)
...	...	...	...
510	20	B1(Zero)	A2(Old)
690	20	B2(Four)	A2(Old)
810	20	B3(Eight)	A2(Old)

(More info appears at the original post.)

An advantage of Bayesian analysis:
The original post showed that the main effect of age, that is, the between-subject factor, was credibly non-zero, which agreed with the result from NHST, which had a p value a little under .05. The estimated magnitude of difference between Old and Young closely matched the marginal means in the data. But the 95% HDI on the difference was very precise compared with the NHST confidence interval. In other words, the Bayesian analysis was much more powerful. The diference was dramatic, so I expressed some doubt in the original post. But I am now convinced that the difference is real and correct. Essentially, the Bayesian analysis estimates all the parameters simultaneously, and creates a single, fixed posterior distribution over multi-dimensional parameter space. We then examine the posterior from difference perspectives, such as, for example, collapsing across all dimensions except Old minus Young, or collapsing across all dimensions except Four degrees minus Zero degrees. We do not "re-scale" the posterior for different perspectives on the parameters. In NHST, on the other hand, different tests can have different error terms in their F ratios, which means that different comparisons are scaled differently. In particular, the F ratio for Old versus Young uses a different error term (i.e., denominator) than the F ratio for Four degrees versus Zero degrees, and it turns out that the former error term is larger than the latter error term, hence the former test is not as powerful, relatively speaking. Bayes is better!

The models in the Bayesian analysis and in classical ANOVA:
In classical ANOVA, the model analyzes the data variance into five components plus residual noise. (See Maxwell & Delaney, Ch. 12, cited above.) The five components are:  (1) the (between-subect) main effect, A, (2) the (within-subject) main effect, B, (3) the main effect of subject within levels of A, S/A, (4) the interaction AxB, and (5) the interaction of B with subjects within levels of A, BxS/A. It turns out that the five components actually use up all the variance, so there is zero residual noise remaining. Another way of thinking about it is that the BxS/A interaction term cannot be identified separately from the noise, because there is only one measurement per cell of the design. (That is also why the BxS/A term is used as the error term for some of the F ratios.) Therefore the model I've used in the Bayesian analysis does not include a BxS/A term:

  for ( i in 1:Ntotal ) {
    y[i] ~ dnorm( mu[i] , tau )
    mu[i] <- base + a[aLvl[i]] + s[sLvl[i]] + b[bLvl[i]] + axb[aLvl[i],bLvl[i]]
    # The model has no BxS term because that would leave zero noise variance.
  }

 The model remains unchanged from the original program; the news here is explicitly explaining it.

The corrected contrast analysis:
The original post included a few different contrast analyses. One was programmed incorrectly, because I mistakenly put it in the section for interaction contrasts, instead of creating a new section for so-called "simple" contrasts. While correcting the code, I also re-expressed the contrasts in the more meaningful new format reported at this previous post. Thus, instead of just a matrix of numerical contrast coefficients without clear meaning, the new code uses logical referencing with the level names, like this:

  simpleContrastList = list(
    A1B1vA2B1 = ( outer(aLvlNames=="A2(Old)",bLvlNames=="B1(Zero)")
                  - outer(aLvlNames=="A1(Young)",bLvlNames=="B1(Zero)") )
  )

That code simply means to compute the difference of "A2(Old),B1(Zero)" and "A1(Young),B1(Zero)", that is, the difference of Old and Young at Zero degrees angle. If you haven't previously tried programming a contrast, that code might still look mysterious, but once you get the hang of it, it's more meaningful and resistant to inadvertent re-ordering of levels than the old format:

  simpleContrastList = list(
    A1B1vA2B1 = matrix( c(1,0,0,-1,0,0) , nrow=2 , byrow=TRUE )
  )

While that old form is shorter, it is less meaningful because it does not show the names of the levels being referred to, and it is easily broken if the levels get re-ordered by different operating system conventions for alphabetizing. One more change: The computation of the simple contrast, at the end of the program, relies on a new section of code.

Other revisions in the program:
I also changed the prior specification in the model, as explained at this previous post. For example, here is the prior on the main effect of A:

  for ( j in 1:NaLvl ) { a[j] ~ dnorm( 0.0 , aTau ) }
  aTau <- 1 / pow( aSD , 2 )
  aSD ~ dgamma(1.221,0.003683) # mode=60,sd=300. Change for scale of data!

The estimate of the standard deviation of the A effect, aSD, has a gamma prior that has a mode at 60 with declining density toward zero, instead of a "generic" uniform or folded-t or gamma that has notable mass near zero.

Thanks again to Wolf for finding the error in the contrast analysis and spurring the revisions!

Get the revised program here and the data file here.

Week-long Workshop, June 11-15

I'll be doing a week-long workshop at the Inter-university Consortium for Political and Social Research (ICPSR), at the University of Michigan, Ann Arbor, June 11-15. Details are here.


A list of future and past workshops can be found here.

Graphical model diagrams in Doing Bayesian Data Analysis versus traditional convention

In this post I contrast conventions for illustrating hierarchical models. On the one hand, there is the traditional convention as used, for example, by DoodleBUGS. On the other hand, there is the style used in Doing Bayesian Data Analysis (DBDA). I explain the advantages of the style in DBDA.

Consider a generic model for Bayesian linear regression. The graphical model diagram in DBDA looks like this:

Graphical diagram in Doing Bayesian Data Analysis.

A corresponding graphical model diagram in DoodleBUGS looks something like this:

Graphical diagram from DoodleBUGS.

The DoodleBUGS diagrams are much like conventional graphical diagrams used in computer science and statistics.

Which diagram is better for explaining the model? For me, it's the diagrams in DBDA.

• The diagrams in DBDA show at a glance what the distribution is for each variable. By contrast, the diagrams in DoodleBUGS do not show the distributions at all. Instead, you have to cross reference the equations, shown elsewhere.
• The diagrams in DBDA show which parameters "live together" in the same distribution. For example, μ_i and τ are seen to be the mean and precision of the same normal distribution. By contrast, the diagrams in DoodleBUGS do not show which distributions the parameters "live in". For example, we do not know from the diagram whether μ_i and τ are in the same distribution or not. To find out, you have to look the equations, shown elsewhere.
• There are other explanatory advantages of the format in DBDA. In particular, the icons of the distributions show directly whether a variable is discrete or continuous, and its range. For example, the icon of the gamma distribution shows that the variable is continuous and has a lower bound. The icon of the Bernoulli distribution (not illustrated here, but repeatedly in the book) shows that the variable has two discrete values. By contrast, conventional diagrams like DoodleBUGS indicate continuous versus discrete by the arbitrary shape of the figure that surrounds the variable: oval for continuous and square for discrete. Or was it oval for discrete and square for continuous? It's easy to get confused by arbitrary conventions.

Which diagram is better for understanding the corresponding JAGS/BUGS model specification? For me, it's the diagrams in DBDA. The key reason is that the diagrams in DBDA have a much more direct correspondence to lines of code in JAGS/BUGS: (Usually) each arrow in the DBDA diagram corresponds to a line of code in the JAGS/BUGS model specificaion. Notice in the DBDA diagram above, there are five arrows. Each arrow has a corresponding line of code in the model specification:

Notice that the DoodleBUGS diagram also has five arrows, but those arrows have no direct correspondence to the model specification! In particular, there is no line of code that says y is related to tau, and a separate line of code that says y is related mu, and a separate line of code that says mu is related to alpha, and another line of code that says mu is related to beta.

The style of diagrams in DBDA are a direct expression of the conceptual distributions and dependencies in the model. And, if you can draw such a picture, it is relatively straightforward to express it in JAGS/BUGS. But the conventional diagrams like DoodleBUGS leave out a huge amount of important conceptual information, and provide little guidance for how to express the model in JAGS/BUGS. Thus, both pedagogically and practically, I prefer the diagrams in DBDA.

One thing that might be improved in the DBDA diagrams is the specification of iteration. In its current form, iteration is indicated ambiguously with an ellipsis that does not indicate explicitly which index is being iterated. In some hierarchical models it can be unclear which index is implied. This could be clarified by using some sort of "plate" notation like what is used in DoodleBUGS, but when plates are drawn in the DBDA diagrams, the overall effect gets visually messy. A simple fix is simply to indicate the index and its limits next to the ellipsis.

Hierarchical diagrams read bottom to top; JAGS/BUGS code reads top to bottom

Consider a generic model for simple linear regression. The data are metric values, modeled as coming from a normal distribution that has mean parameter μ=β₀+β₁x₁ and precision parameter τ (=1/σ²). The priors on the intercept and slope parameters (β₀ and β₁) are normal, and the prior on the precision is gamma.

Notice that the description of the model started with the nature of the data, then described the likelihood function, then described the prior. This is the sequential order of description that makes sense for communicating to people. First you have to know the nature of the data being modeled. Next, you have to know the choice of likelihood function. For example, the metric data might have been modeled by a normal distribution, or by a log-normal distribution, or by a Weibull distribution, or by a t distribution, or whatever. Each of those likelihood functions has different parameters. Once the likelihood function is specified, with its corresponding parameters, then it makes sense to talk about the prior on those parameters.

The JAGS/BUGS code, in all the book's programs, specifies the model details in that order: from data, to likelihood, to prior. For example, here is the model specification for simple linear regression:

But, unlike the JAGS/BUGS code, the hierarchical diagrams in the book put the data at the bottom and the priors on the top. This might feel "upside down" relative to the JAGS/BUGS code, but the diagrams are forced to be this way because of pre-existing conventions for drawing probability distributions. The convention is to put the parameter axis on the abscissa (x axis), with the probability density on the ordinate (y axis). Therefore the parameter being modeled must be oriented at the bottom, and the parameters describing the density must be at the top, like this:

Therefore, the hierarchical diagrams should always be read starting at the bottom, then working upward.

How to report a Bayesian analysis: Teaching why

An interesting recent article emphasized that asking students to generate what should be reported from a Bayesian analysis also gets them to think about why things need to be reported, which in turn can get students to understand better how Bayesian analysis works and what it means. In this blog post I briefly summarize the article, compare it with the recommendations for reporting a Bayesian analysis in Doing Bayesian Data Analysis, and suggest that there are some important points for reporting that might be difficult for beginning students to generate on their own.

The article is: Pullenayegum, E. M., Guo, Q., & Hopkins, R. B. (2012). Developing critical thinking about reporting of Bayesian analyses. Journal of Statistics Education, 20(1). It's available at this link. Here are some excerpts:

[Abstract:] Whilst there are published guidelines on reporting of Bayesian analyses, students should also be encouraged to think about why some items need to be reported whereas others do not. We describe a classroom activity in which students develop their own reporting guideline. ... [Section 1:] Since Bayesian analyses are far less widely used in medicine [than frequentist analyses], it is difficult for students to gauge what is typical. Thus, teaching students how to report Bayesian analyses in the medical literature is an important component of a course in Bayesian biostatistics. When teaching reporting, we need to avoid training students to follow a set of rules unthinkingly. Rather we need to focus on helping students to think critically about what is needed. That is, we need to teach not just the “what”, but also the “why”. ... [Section 4.4:] Two of us (RBH and QG) participated in the first implementation of the exercise as students. As the exercise progressed, we found ourselves thinking as readers, reviewers or editors rather than as the statistician or author. ... [Section 5:] The value of the activity is in the learning process rather than the guideline itself.

The exercise itself consists of students anonymously generating candidate items for inclusion, then having the items collated onto a master list of candidates, then rating the items for importance and discussing why they are important. (See the article for details about the group dynamic.) Importantly, but perhaps not emphasized enough in the article, the instructor can (and did) anonymously contribute items to the list during the first round. This strikes me as a very useful exercise for students, and I may try some variation of it myself next time I teach my course.

The article reports the lists of items generated by two different classes. The lists included points about the prior distributions, the likelihood function, the analysis technique, and the results. Please see Table 1 of the article for details. Although the emphasis of the article was on getting students to think about why items should or need not be reported, rather than on the actual list created, it is still informative to see what items the students settled on, and whether anything went missing that might be considered to be important.

In particular, it's natural for me to compare the student-generated lists with my own recommendations in Doing Bayesian Data Analysis (Ch. 23, pp. 620-622):

There is notable overlap with items in the student-generated lists, but the first two "essential" points raised in DBDA were not emphasized by the students. These points are (1) Motivate the use of Bayesian (non-NHST) analysis, and (2) Clearly describe the model and its parameters. Both of these points are about reporting the forest before reporting the trees. Both of these points are about contextualizing the analysis and giving it meaning. In particular, the second point entails the idea that the model is a particular description of data, selected from the space of all possible models because it is meaningful in the particular context. Finally, the "essential" points in DBDA are meant to be reported in sequence. This temporal, sequential order of points is important for the comprehensibility of the report. For example, the likelihood function and its parameters must be explained before the prior and its parameters can be explained. (And the structure of the data must be explained before the likelihood function can be described.)

I think that all these issues ---motivating use of Bayesian analysis, describing the model and parameters, and reporting in a particular sequential order--- are about understanding the larger context in which statistical analysis resides, and this larger context might be relatively difficult for beginning students to apprehend. Therefore instructors who adopt the exercise, of students generating guidelines for reporting, may want to seed the candidate list with these sorts of items, or at least be sure that they are brought up during discussion.