Workshop on doing Bayesian data analysis at Indiana University

Workshop on doing Bayesian data analysis at Indiana University's Workshop in Methods, Friday Oct. 5, 2:00pm. See details here.

A list of some previous workshops is here.

From BUGS with BRugs to JAGS with rjags

As mentioned in several previous posts, I strongly recommend using JAGS instead of BUGS, and I have converted all the BUGS programs to JAGS versions. Here I provide guidelines for how to make the conversion in case you want to convert your own programs.

For a concrete example, I will use the programs BernTwoBugs.R and BernTwoJags.R. I’ll proceed section by section through the programs.

The header:

BUGS + BRugs version:

library(BRugs)

JAGS + rjags version:

require(rjags)

Instead of “require” it could say “library”. Also in the JAGS + rjags version I added a way for the graphics to work on non-Windows machines. This is just R, so it can work with BUGS too:

if ( .Platform$OS.type != "windows" ) {

  windows <- function( ... ) X11( ... )

}

The model specification:

BUGS + BRugs version:

modelstring = "

# BUGS model specification begins here...

model {

    # Likelihood. Each flip is Bernoulli.

    for ( i in 1 : N1 ) { y1[i] ~ dbern( theta1 ) }

    for ( i in 1 : N2 ) { y2[i] ~ dbern( theta2 ) }

    # Prior. Independent beta distributions.

    theta1 ~ dbeta( 3 , 3 )

    theta2 ~ dbeta( 3 , 3 )

}

# ... end BUGS model specification

" # close quote for modelstring

# Write model to a file:

.temp = file("model.txt","w") ; writeLines(modelstring,con=.temp) ; close(.temp)

# Load model file into BRugs and check its syntax:

modelCheck( "model.txt" )

JAGS + rjags version:

modelString = "

# JAGS model specification begins here...

model {

    # Likelihood. Each flip is Bernoulli.

    for ( i in 1 : N1 ) { y1[i] ~ dbern( theta1 ) }

    for ( i in 1 : N2 ) { y2[i] ~ dbern( theta2 ) }

    # Prior. Independent beta distributions.

    theta1 ~ dbeta( 3 , 3 )

    theta2 ~ dbeta( 3 , 3 )

}

# ... end JAGS model specification

" # close quote for modelstring

# Write the modelString to a file, using R commands:

writeLines(modelString,con="model.txt")

Notice that the model specification is the same in JAGS as in BUGS. Also, in both cases the modelString gets written to a file called “model.txt”. The JAGS + rjags version uses a streamlined version of writeLines that would also work in the BUGS program, as it is just an R command. The only difference is in how the specification gets communicated to BUGS or JAGS: BRugs uses the modelCheck command, but there is no analogous command in rjags.

The data:

BUGS + BRugs version:

# Specify the data in a form that is compatible with BRugs model, as a list:

datalist = list(

    N1 = 7 ,

    y1 = c( 1,1,1,1,1,0,0 ) ,

    N2 = 7 ,

    y2 = c( 1,1,0,0,0,0,0 )

)

# Get the data into BRugs:

modelData( bugsData( datalist ) )

JAGS + rjags version:

# Specify the data in a form that is compatible with JAGS model, as a list:

dataList = list(

    N1 = 7 ,

    y1 = c( 1,1,1,1,1,0,0 ) ,

    N2 = 7 ,

    y2 = c( 1,1,0,0,0,0,0 )

)

The specification of the data is the same in JAGS as in BUGS. The only difference is in how the specification gets communicated to BUGS or JAGS.: BRugs uses the modelData command, but there is no analogous command in rjags.

Initialize the chains:

BUGS + BRugs version:

modelCompile()

modelGenInits()

JAGS + rjags version:

# Can be done automatically in jags.model() by commenting out inits argument.

# Otherwise could be established as:

# initsList = list( theta1 = sum(dataList$y1)/length(dataList$y1) ,

#                   theta2 = sum(dataList$y2)/length(dataList$y2) )

The BUGS version has to compile the model (using the BRugs modelCompile command) and then generate initial values (using the BRugs modelGenInits command). The JAGS version does not need any explicit initialization at this point, as the commented code explains.

Run the chains:

BUGS + BRugs version:

samplesSet( c( "theta1" , "theta2" ) ) # Keep a record of sampled "theta" values

chainlength = 10000                     # Arbitrary length of chain to generate.

modelUpdate( chainlength )             # Actually generate the chain.

JAGS + rjags version:

parameters = c( "theta1" , "theta2" )     # The parameter(s) to be monitored.

adaptSteps = 500              # Number of steps to "tune" the samplers.

burnInSteps = 1000            # Number of steps to "burn-in" the samplers.

nChains = 3                   # Number of chains to run.

numSavedSteps=50000           # Total number of steps in chains to save.

thinSteps=1                   # Number of steps to "thin" (1=keep every step).

nIter = ceiling( ( numSavedSteps * thinSteps ) / nChains ) # Steps per chain.

# Create, initialize, and adapt the model:

jagsModel = jags.model( "model.txt" , data=dataList , # inits=initsList ,

                        n.chains=nChains , n.adapt=adaptSteps )

# Burn-in:

cat( "Burning in the MCMC chain...\n" )

update( jagsModel , n.iter=burnInSteps )

# The saved MCMC chain:

cat( "Sampling final MCMC chain...\n" )

codaSamples = coda.samples( jagsModel , variable.names=parameters ,

                            n.iter=nIter , thin=thinSteps )

# resulting codaSamples object has these indices:

#   codaSamples[[ chainIdx ]][ stepIdx , paramIdx ]

Roughly the equivalent of BRugs modelCompile is rjags jags.model. For burning in, the rough equivalent of BRugs modelUpdate before samplesSet  is rjags update. Notice that the BUGS version here did no burning in. For the final chain, the rough equivalent of BRugs modelUpdate is rjags coda.samples. Notice that rjags specifies the parameters to be stored with the variable.names argument in the coda.samples command, whereas BRugs specifies the parameters in its samplesSet command.

Examine the results:

BUGS + BRugs version:

theta1Sample = samplesSample( "theta1" ) # Put sampled values in a vector.

theta2Sample = samplesSample( "theta2" ) # Put sampled values in a vector.

# Plot the trajectory of the last 500 sampled values.

…

JAGS + rjags version:

# Convert coda-object codaSamples to matrix object for easier handling.

# But note that this concatenates the different chains into one long chain.

# Result is mcmcChain[ stepIdx , paramIdx ]

mcmcChain = as.matrix( codaSamples )

theta1Sample = mcmcChain[,"theta1"] # Put sampled values in a vector.

theta2Sample = mcmcChain[,"theta2"] # Put sampled values in a vector.

# Plot the trajectory of the last 500 sampled values.

…

Once the chain is put into variables in R, they can be plotted the same way.

One big difference not shown above is how the chains can be examined for autocorrelation and convergence. My homegrown plotChains function uses BRugs commands and will not work with the JAGS output. Instead, JAGS+rjags returns the chain as a coda-package object, named codaSamples above. There are many useful functions in the coda package for displaying the chains, not shown above. For example, summary( codaSamples ), plot( codaSamples ), and autocorr.plot( codaSamples ).

Posterior predictive check can and should be Bayesian

Perception apparently employs prior knowledge that illumination comes from above, and that the surface itself has constant color.

Here's a new article, in press. I'm a bit reluctant about it because it got zero feedback and is unchanged from the initial submission, but, damn the torpedos ..., fools rush in ..., and all that sort of thing.

Abstract: Bayesian inference is conditional on the space of models assumed by the analyst. The posterior distribution indicates only which of the available parameter values are less bad than the others, without indicating whether the best available parameter values really fit the data well. A posterior predictive check is important to assess whether the posterior predictions of the least bad parameters are discrepant from the actual data in systematic ways. Gelman and Shalizi (2012a) assert that the posterior predictive check, whether done qualitatively or quantitatively, is non-Bayesian. I suggest that the qualitative posterior predictive check might be Bayesian, and the quantitative posterior predictive check should be Bayesian. In particular, I show that the “Bayesian p value,” from which an analyst attempts to reject a model without recourse to an alternative model, is ambiguous and inconclusive. Instead, the posterior predictive check, whether qualitative or quantitative, should be consummated with Bayesian estimation of an expanded model. The conclusion agrees with Gelman and Shalizi (2012a) regarding the importance of the posterior predictive check for breaking out of an initially assumed space of models. Philosophically, the conclusion allows the liberation to be completely Bayesian instead of relying on a non-Bayesian deus ex machina. Practically, the conclusion cautions against use of the Bayesian p value in favor of direct model expansion and Bayesian evaluation.

Kruschke, J. K. (in press). Posterior predictive check can and should be Bayesian: Comment on Gelman and Shalizi (2012a). British Journal of Mathematical and Statistical Psychology.
Get the full manuscript here.

One-group version of BEST (Bayesian estimation supersedes the t test)

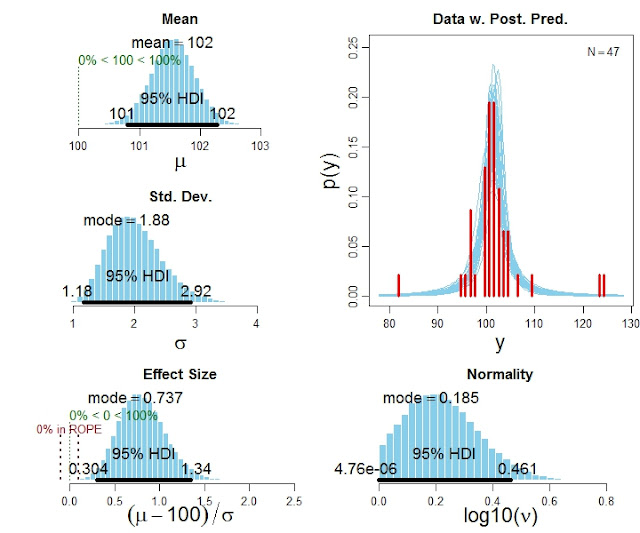
The in-press article, Bayesian estimation supersedes the t test, focuses on the two-group case. Various readers have wanted a one-group version, which is now available. It is in the zip file with the two-group programs.

Here is an example of the code for using the program:

# Specify the data
y = c(101,100,102,104,102,97,105,105,98,101,100,123,105,103,100,95,102,106,
       109,102,82,102,100,102,102,101,102,102,103,103,97,97,103,101,97,104,
       96,103,124,101,101,100,101,101,104,100,101)

# Run the Bayesian analysis:
source("BEST1G.R")
mcmcChain = BEST1Gmcmc( y )

# Display the results:
BEST1Gplot( y , mcmcChain , compValm=100 , ROPEeff=c(-0.1,0.1) , pairsPlot=TRUE )

The function BEST1Gplot returns detailed numerical summaries of the posterior distribution (not shown here), and it also produces graphical output like this: