Abelson's paradox, baseball, null differences, the ROPE, and hierarchical Bayesian analysis

In a thread elsewhere, a reader of Bayesian estimation supersedes the t test commented: "Doesn't Abelson's paradox preclude the establishment of guidelines for a sufficiently small effect size?"  In this post I briefly review Abelson's paradox and demonstrate how hierarchical Bayesian data analysis is actually applied to real baseball data of the type that Abelson used to illustrate his paradox. Bayesian estimation provides rich estimates of the abilities of players and their differences. There is no paradox.

First, a cursory review of Abelson's paradox. It was described in a brief article: Abelson, R. P. (1985). A variance explanation paradox: When a little is a lot. Psychological Bulletin, 97(1), 129-133. Abelson considered the batting averages of major league baseball players. A batting average is simply the ratio of number of hits to number of at-bats. In the 2012 season, players each had about 550 opportunities at bat, and typically got about 150 hits, for a typical batting average of about 0.27. Across 143 different players, the batting averages ranged from about 0.19 to 0.34. (Data from ESPN.) Abelson was concerned with whether that variation across players was large compared to the variation within players; in other words, he wanted to know the magnitude of the proportion of variance accounted for by player ability. He came up with a mathematical approximation and argued that for typical data the magnitude of the proportion of variance accounted for is about 0.003. The "paradox" is that such a small number conflicts with sports fans' intuition that player ability should account for a lot more of the variance of hits. Abelson discussed the meaning of his calculation and how it differs from the everyday intuition of the sports fan, saying that his statistic refers to the predictability of a single at-bat. But I can't say I fully understand what Abelson was going for, and the Bayesian analysis of real data (shown below) seems clear and unparadoxical to me.

What does any of that have to do with Bayesian data analysis? Presumably the reader who commented about Abelson's paradox was thinking about the approach to null values that I and others have advocated, whereby a null value for a parameter is deemed accepted for practical purposes if its 95% highest density interval (HDI) falls entirely within a region of practical equivalence (ROPE) around the null value. Perhaps the reader was concerned that no ROPE can be established because even tiny values, like Abelson's 0.003, can correspond to intuitively large effects.

Perhaps the best rebuttal is simply to demonstrate how to do a Bayesian analysis of batting averages, including a ROPE. The analysis uses a hierarchical model that simultaneously estimates individual player abilites and the overall average ability of major league players.

The model comes directly from Chapter 9 of Doing Bayesian Data Analysis. (For an example of applying the same model to meta-analysis of ESP data, see this post. That post also includes a hierarchical diagram of the model.) In the model, the i-th player has an underlying probability of getting a hit, denoted theta[i]. The value of theta[i] is estimated from observing the number of hits y[i] and at-bats N[i] for each player. Importantly, the model assumes that the theta[i] come from a higher-level distribution that describes the individual differences among major league players. There is an overall central tendency, mu, for the batting average of major league players, and a "tightness" of clustering around that central tendency, denoted kappa. (For details, please see Ch. 9 of DBDA.)

The hierarchical structure of the model provides shrinkage in the estimates of the individual abilities. Essentially, each player's data inform the estimate of theta[i] for that player, but also inform the group-level parameters mu and kappa, which in turn influence the estimated values of theta[.] for other players. Thus, if many players all have batting averages right around .27, the group-level distribution is estimated to be very "tight," which pulls in (shrinks) outlying individuals toward the group average. This is intuitively reasonable: If you have information that player after player has an average around .27, you should use that information to inform your estimate of the next player.

When making decisions about differences in estimated abilities, what sort of ROPE is meaningful? There is no single correct answer because it depends on practical consequences. But suppose we say that a difference of 10 hits, in a season of 550 at bats, has practical significance. The ratio 10/550 is just under 0.02, so let's establish a ROPE as -0.02 to +0.02. Our decision rule for assessing differences between players is now this: The difference in abilities between players is deemed to be credibly and practically different from zero if the 95% HDI on the estimated difference falls completely outside a ROPE from -0.20 to +0.02. The difference in abilities is deemed to be practically equivalent to zero if the 95% HDI on the estimated difference falls completely inside the ROPE.

Here are some results from the analysis. First, consider the players with the highest and lowest batting average during the 2012 regular season:

The right panel shows that their abilities (in terms of estimated probability of getting a hit at bat) are credibly different, and the posterior distribution reveals in detail the relative credibility of the whole range of candidate differences. The graphs also plot the observed batting average (y[i]/N[i]) as small red +'s on the abscissa. Notice that the estimated theta values show clear shrinkage toward the group average. Thus, although Buster Posey had a batting average of 0.336, the estimate of the underlying probability of getting a hit is shrunken toward the major league average, with a mean estimate of 0.313. Similarly, although Carlos Pena had a batting average of 0.197, the estimate of the underlying probability of getting a hit is shrunken toward the central tendency of the group, with a mean estimate of 0.225. Despite the shrinkage, the difference (right panel) is still credibly non-zero.

Here are the results for the two players in the middle of the pack:

The right panel shows that the estimated difference in their underlying probabilities of getting a hit is nearly zero. 52% of the posterior distribution falls within the ROPE. Thus, we do not have enough precision in the estimate of the differences to declare that their abilities are equal for practical purposes, where "practical" is defined in terms of this choice of ROPE.

Thus, Bayesian analysis provides rich and meaningful inferences about the sort of data that Abelson was interested in. I don't see any "paradox" that needs to be overcome. The Bayesian analysis never even brought up the issue of "proportion of variance accounted for" as Abelson did. Because the Bayesian analysis directly estimates all the parameters of interest, and provides a complete posterior distribution for their credibilities, Abelson's paradoxical statistic never even arose.


Appendix: The complete program. Data are from ESPN, linked in text above.

rm(list = ls())
graphics.off()
fileNameRoot="MajorLeagueBaseballBattingJAGS"
if ( .Platform$OS.type != "windows" ) {
  windows <- function( ... ) X11( ... )
}
                       # In the style of:
require(rjags)         # Kruschke, J. K. (2011). Doing Bayesian Data Analysis:
                       # A Tutorial with R and BUGS. Academic Press / Elsevier.
#------------------------------------------------------------------------------
# THE MODEL.

# Specify the model in JAGS language, but save it as a string in R:
modelString = "
model {
    # Likelihood:
    for ( i in 1:nPlayers ) {
        y[i] ~ dbin( theta[i] , N[i] )
    }
    # Prior:
    for ( i in 1:nPlayers ) {
        theta[i] ~ dbeta( a , b )
    }
    a <- mu * kappa
    b <- ( 1.0 - mu ) * kappa
    mu ~ dbeta( 1,1 )
    kappa ~ dgamma( 1.393 , 0.0393 ) # mode=10, sd=30
}
# ... JAGS model specification ends.
" # close quote to end modelString
# Write the modelString to a file, using R commands:
writeLines(modelString,con="model.txt")

#------------------------------------------------------------------------------
# THE DATA.

dataFrame = read.csv( file="MajorLeagueBaseballBattingStats2012.csv" )

y = dataFrame$H  # hits for each player
N = dataFrame$AB  # at bats for each player
nPlayers = length(y)

dataList = list(
    y = y ,
    N = N ,
    nPlayers = nPlayers
)

#------------------------------------------------------------------------------
# INTIALIZE THE CHAIN.

# Let JAGS do it randomly...

#------------------------------------------------------------------------------
# RUN THE CHAINS.

parameters = c( "mu" , "kappa" , "theta" )   # The parameter(s) to be monitored.
adaptSteps = 1000              # Number of steps to "tune" the samplers.
burnInSteps = 1000            # Number of steps to "burn-in" the samplers.
nChains = 3                   # Number of chains to run.
numSavedSteps=100000           # Total number of steps in chains to save.
thinSteps=1                   # Number of steps to "thin" (1=keep every step).
nIter = ceiling( ( numSavedSteps * thinSteps ) / nChains ) # Steps per chain.
# Create, initialize, and adapt the model:
jagsModel = jags.model( "model.txt" , data=dataList , # inits=initsList ,
                        n.chains=nChains , n.adapt=adaptSteps )
# Burn-in:
cat( "Burning in the MCMC chain...\n" )
update( jagsModel , n.iter=burnInSteps )
# The saved MCMC chain:
cat( "Sampling final MCMC chain...\n" )
codaSamples = coda.samples( jagsModel , variable.names=parameters ,
                            n.iter=nIter , thin=thinSteps )
# resulting codaSamples object has these indices:
#   codaSamples[[ chainIdx ]][ stepIdx , paramIdx ]

#------------------------------------------------------------------------------
# EXAMINE THE RESULTS.

checkConvergence = FALSE
if ( checkConvergence ) {
  autocorr.plot( codaSamples , ask=T )
}

# Convert coda-object codaSamples to matrix object for easier handling.
# But note that this concatenates the different chains into one long chain.
# Result is mcmcChain[ stepIdx , paramIdx ]
mcmcChain = as.matrix( codaSamples )

# Extract the posterior sample from JAGS for easier reference:
mu = mcmcChain[,"mu"]
kappa = mcmcChain[,"kappa"] # BRugs gets sample from JAGS
theta = matrix( 0 , nrow=nPlayers , ncol=nChains*nIter )
for ( i in 1:nPlayers ) {
    nodeName = paste( "theta[" , i , "]" , sep="" )
    theta[i,] = mcmcChain[,nodeName]
}

# Make a graph using R commands:
source("plotPost.R")

windows(width=7,height=2.5)
layout( matrix( 1:2 , nrow=1 , byrow=TRUE ) )
#par(mar=c(2.95,2.95,1.0,0),mgp=c(1.35,0.35,0),oma=c( 0.1, 0.1, 0.1, 0.1) )
plotPost( mu , xlab="mu" , main="Group Mean" )
plotPost( kappa , xlab="kappa" , main="Group Certainty" )
savePlot( file=paste(fileNameRoot,"MuKappa",sep="") , type="jpg" )

plotPlayerDiff = function( idx1 , idx2 , diffRope=c(-0.02,0.02) , savePlotFile=FALSE ) {
  windows(width=7,height=2.5)
  layout( matrix( 1:3 , nrow=1 , byrow=TRUE ) )
  #par(mar=c(2.95,2.95,1.0,0),mgp=c(1.35,0.35,0),oma=c( 0.1, 0.1, 0.1, 0.1) )
  plotPost( theta[idx1,] , xlab=paste("theta",idx1) , main=dataFrame$PLAYER[idx1] )
  points( dataFrame$AVG[idx1] , 0 , pch="+" , col="red" , cex=1.5 )
  plotPost( theta[idx2,] , xlab=paste("theta",idx2) , main=dataFrame$PLAYER[idx2] )
  points( dataFrame$AVG[idx2] , 0 , pch="+" , col="red" , cex=1.5)
  plotPost( theta[idx1,] - theta[idx2,] ,
            xlab=paste("theta",idx1,"-","theta",idx2) , main="Difference" ,
            compVal=0.0 , ROPE=diffRope )
  points( dataFrame$AVG[idx1]-dataFrame$AVG[idx2] , 0 , pch="+" , col="red" , cex=1.5)
  if ( savePlotFile ) {
    savePlot( file=paste(fileNameRoot,"Theta",idx1,"Theta",idx2,sep="") , type="jpg" )
  }
}
plotPlayerDiff(1,nPlayers,savePlotFile=TRUE)
plotPlayerDiff( round(nPlayers/2)-1 , round(nPlayers/2) ,savePlotFile=TRUE)

Gamma Likelihood Parameterized by MODE and SD

In a previous post I showed that it's more intuitive to think of a gamma distribution in terms of its mode and standard deviation (sd) than its mean and sd because the gamma distribution is typically skewed. But I did not show how to estimate the mode and sd in the context of a working JAGS/BUGS program, which I do here.

Suppose we have some data, y, that we wish to describe with a gamma distribution. (This requires that all the y values are non-negative, of course.) The dgamma function in JAGS/BUGS and R is parameterized by shape and rate parameters, not by mean, mode, or sd. Therefore we must reparameterize the shape and rate into equivalent mean, mode or sd. If we want to reparameterize by the mean of the gamma distribution, a JAGS/BUGS model statement could look like this:

  model {
    for ( i in 1:N ) {
      y[i] ~ dgamma( sh , ra )
    }
    # parameterized by mean (m) and standard deviation (sd)
    sh <- pow(m,2) / pow(sd,2)
    ra <-     m    / pow(sd,2)
    m ~ dunif(0,100)
    sd ~ dunif(0,100)
  }

If we want to reparameterize by the mode of the gamma distribution, a JAGS/BUGS model statement could look like this:

  model {
    for ( i in 1:N ) {
      y[i] ~ dgamma( sh , ra )
    }
    # parameterized by mode (m) and standard deviation (sd):
    sh <- 1 + m * ra
    ra <- ( m + sqrt( m^2 + 4*sd^2 ) ) / ( 2 * sd^2 )
    m ~ dunif(0,100)
    sd ~ dunif(0,100)
  }
In both model statements, the m parameter is given a dunif(0,100) prior, which implies that the priors in the two models are not equivalent because the mean is not the same as the mode. With vague priors the difference may be inconsequential for the posterior, but it is an important conceptual distinction. In fact, the whole point of reparameterizing is to make the prior more intuitive to specify! It's more intuitive, for most of us, to put a meaningful prior on the mode and sd than on the shape and rate.

Here are the results for the two models:

The left panels show the data (which are the same for both models) with a smattering of posterior predicted gamma distributions superimposed. The upper row shows the estimates for the model parameterized by the mean and sd, while the lower row shows the estimates for the model parameterized by mode and sd. You can see that the estimated mean (about 8.08) is larger than the estimated mode (about 7.01), but the estimated sd is essentially the same in the two models.


Appendix: Full program listed here, merely FYI.

graphics.off()
rm(list=ls(all=TRUE))
fileNameRoot="GammaModeJags" # for constructing output filenames
if ( .Platform$OS.type != "windows" ) {
  windows <- function( ... ) X11( ... )
}
require(rjags)         # Kruschke, J. K. (2011). Doing Bayesian Data Analysis:
                       # A Tutorial with R and BUGS. Academic Press / Elsevier.
#------------------------------------------------------------------------------
# THE MODEL.

mType = c("Mean","Mode")[1]

if ( mType == "Mean" ) {
  modelstring = "
  model {
    for ( i in 1:N ) {
      y[i] ~ dgamma( sh , ra )
    }
    # parameterized by mean (m) and standard deviation (sd)
    sh <- pow(m,2) / pow(sd,2)
    ra <-     m    / pow(sd,2)
    m ~ dunif(0,100)
    sd ~ dunif(0,100)
  }
  " # close quote for modelstring
} 

if ( mType == "Mode" ) {
  modelstring = "
  model {
    for ( i in 1:N ) {
      y[i] ~ dgamma( sh , ra )
    }
    # parameterized by mode (m) and standard deviation (sd):
    sh <- 1 + m * ra
    ra <- ( m + sqrt( m^2 + 4*sd^2 ) ) / ( 2 * sd^2 )
    m ~ dunif(0,100)
    sd ~ dunif(0,100)
  }
  " # close quote for modelstring
}
 
# Write model to a file, and send to BUGS:
writeLines(modelstring,con="model.txt")

#------------------------------------------------------------------------------
# THE DATA.

# Load the data:

N = 87 ; m=8 ; sd=3
set.seed(47401)
y = rgamma( N , shape=m^2/sd^2 , rate=m/sd^2 )

# Specify the data as a list:
dataList = list( y = y , N = N )

#------------------------------------------------------------------------------
# INTIALIZE THE CHAINS.

initsList = list( m = mean(y) , sd = sd(y) )

#------------------------------------------------------------------------------
# RUN THE CHAINS

parameters = c( "m" , "sd" ) 
adaptSteps = 1000              # Number of steps to "tune" the samplers.
burnInSteps = 1000            # Number of steps to "burn-in" the samplers.
nChains = 3                   # Number of chains to run.
numSavedSteps=50000           # Total number of steps in chains to save.
thinSteps=1                   # Number of steps to "thin" (1=keep every step).
nPerChain = ceiling( ( numSavedSteps * thinSteps ) / nChains ) # Steps per chain.
# Create, initialize, and adapt the model:
jagsModel = jags.model( "model.txt" , data=dataList , inits=initsList ,
                        n.chains=nChains , n.adapt=adaptSteps )
# Burn-in:
cat( "Burning in the MCMC chain...\n" )
update( jagsModel , n.iter=burnInSteps )
# The saved MCMC chain:
cat( "Sampling final MCMC chain...\n" )
codaSamples = coda.samples( jagsModel , variable.names=parameters ,
                            n.iter=nPerChain , thin=thinSteps )
# resulting codaSamples object has these indices:
#   codaSamples[[ chainIdx ]][ stepIdx , paramIdx ]

#------------------------------------------------------------------------------
# EXAMINE THE RESULTS

checkConvergence = F
if ( checkConvergence ) {
  windows()
  autocorr.plot( codaSamples , ask=F )
}

# Convert coda-object codaSamples to matrix object for easier handling.
# But note that this concatenates the different chains into one long chain.
# Result is mcmcChain[ stepIdx , paramIdx ]
mcmcChain = as.matrix( codaSamples )
chainLength = NROW(mcmcChain)

source("plotPost.R")

windows(width=10,height=3)
layout( matrix(1:3,nrow=1) )
# Data with superimposed posterior predictive gamma's:
hist( y , xlab="y" , ylim=c(0,0.15) , main="Data" , col="grey" , prob=TRUE )
xComb=seq(min(y),max(y),length=501)
nPPC = 15
for ( idx in round(seq(1,chainLength,length=nPPC)) ) {
  if ( mType=="Mean" ) {
    m = mcmcChain[idx,"m"]
    sd = mcmcChain[idx,"sd"]
    sh = m^2 / sd^2
    ra = m   / sd^2
  }
  if ( mType=="Mode" ) {
    m = mcmcChain[idx,"m"]
    sd = mcmcChain[idx,"sd"]
    ra = ( m + sqrt( m^2 + 4*sd^2 ) ) / ( 2 * sd^2 )
    sh = 1 + m * ra
  }
  lines( xComb , dgamma( xComb , sh , ra ) , col="skyblue" , lwd=2 )
}
# Posterior estimates of parameters:
par( mar=c(3,1,2.5,0) , mgp=c(2,0.7,0) )
plotPost( mcmcChain[,"m"] , xlab=mType , main="Posterior Est." , showMode=T )
plotPost( mcmcChain[,"sd"] , xlab="sd" , main="Posterior Est." , showMode=T )
savePlot(file=paste(fileNameRoot,mType,sep=""),type="jpg")

Metropolis Algorithm: Discrete Position Probabilities

I was asked by a reader how I created Figure 7.2 of the book, reproduced at right, which shows the progression of discrete position probabilities at each step in a simple Metropolis algorithm. I couldn't find the original program, so I made a new one, reported here, with an additional example that illustrates a bimodal target distribution.

The main point is mentioned in the middle of p. 128: "At every time step, we multiply the current position probability vector w by the transition probability matrix T to get the position probabilities for the next time step. We keep multiplying by T over and over again to derive the long-run position probabilities. This process is exactly what generated the graphs in Figure 7.2."

The code consists of two main parts. First, build the transition matrix. Second, specify an initial position vector and repeatedly multiply by the transition matrix. Here is the code:


# For Figure 7.2, p. 123 of Doing Bayesian Data Analysis.
fileNameRoot = "DBDAfigure7pt2"

# Specify the target probability distribution.
pTargetName = "Linear" # for filename of saved graph
nSlots = 7
pTarget = 1:nSlots
pTarget = pTarget/sum(pTarget)

# Uncomment following lines for different example
#pTargetName = "Bimodal" # for filename of saved graph
#pTarget = c(1,2,2,1,3,3,1)
#nSlots = length(pTarget)
#pTarget = pTarget/sum(pTarget)

# Construct the matrix of proposal probabilities.
# Row is from position, column is to position.
proposalMatrix = matrix( 0 , nrow=nSlots , ncol=nSlots )
for ( fromIdx in 1:nSlots ) {
  for ( toIdx in 1:nSlots ) {
    if ( toIdx == fromIdx-1 ) { proposalMatrix[fromIdx,toIdx] = 0.5 }
    if ( toIdx == fromIdx+1 ) { proposalMatrix[fromIdx,toIdx] = 0.5 }
  }
}

# Construct the matrix of acceptance probabilities.
# Row is from position, column is to position.
acceptMatrix = matrix( 0 , nrow=nSlots , ncol=nSlots )
for ( fromIdx in 1:nSlots ) {
  for ( toIdx in 1:nSlots ) {
    acceptMatrix[fromIdx,toIdx] = min( pTarget[toIdx]/pTarget[fromIdx] , 1 )
  }
}

# Compute the matrix of overall move probabilities:
moveMatrix = proposalMatrix * acceptMatrix

# Compute the transition matrix, including the probability of staying in place:
transitionMatrix = moveMatrix
for ( diagIdx in 1:nSlots ) {
  transitionMatrix[diagIdx,diagIdx] = 1.0 - sum(moveMatrix[diagIdx,])
}
show( transitionMatrix )

# Specify starting position vector:
positionVec = rep(0,nSlots)
positionVec[round(nSlots/2)] = 1.0

# Loop through time steps and display position probabilities:
windows(height=7,width=7) # change to x11 for non-WindowsOS
layout( matrix(1:16,nrow=4) )
par( mar = c( 2.8 , 2.8 , 1.0 , 0.5 ) , mgp = c( 1.4 , 0.5 , 0 ) )
for ( timeIdx in 1:15 ) {
  # Display position probability:
  plot( 1:nSlots , positionVec , xlab="Position" , ylab="Probability" ,
        type="h" , lwd=5 , col="skyblue" )
  text( 1 , max(positionVec) , bquote(t==.(timeIdx)) , adj=c(0,1) )
  # Update next position probability:
  positionVec = positionVec %*% transitionMatrix
}
# Plot target distribution
plot( 1:nSlots , pTarget , xlab="Position" , ylab="Probability" ,
      type="h" , lwd=5 , col="skyblue" )
text( 1 , max(positionVec) , bquote(target) , adj=c(0,1) )

savePlot( filename=paste(fileNameRoot,pTargetName,sep="") , type="jpg" ) 

For the linearly increasing target distribution, the transition matrix looks like this:

     [,1]      [,2]      [,3]  [,4]      [,5]       [,6]      [,7]
[1,] 0.50 0.5000000 0.0000000 0.000 0.0000000 0.00000000 0.0000000
[2,] 0.25 0.2500000 0.5000000 0.000 0.0000000 0.00000000 0.0000000
[3,] 0.00 0.3333333 0.1666667 0.500 0.0000000 0.00000000 0.0000000
[4,] 0.00 0.0000000 0.3750000 0.125 0.5000000 0.00000000 0.0000000
[5,] 0.00 0.0000000 0.0000000 0.400 0.1000000 0.50000000 0.0000000
[6,] 0.00 0.0000000 0.0000000 0.000 0.4166667 0.08333333 0.5000000
[7,] 0.00 0.0000000 0.0000000 0.000 0.0000000 0.42857143 0.5714286

The row is the "from" position and the column is the "to" position. For example, the probability of moving from position 4 to position 3 is 0.375. 

The resulting graph looks like this:

If you uncomment the lines that specify a bimodal target, the resulting graph looks like this:

Program updates and changes

The plotPost() function, which plots histograms of MCMC chains annotated with HDI and other info, was changed a few weeks ago. plotPost() now returns summary information about the chain instead of summary information about the histogram.  A reader caught a conflict this caused in the program BernMetropolisTemplate.R, which has now been changed to accommodate the new plotPost(). The new programs can be found at the usual site: http://www.indiana.edu/~kruschke/DoingBayesianDataAnalysis/Programs/?M=D.The zip file with all the programs has also been updated. Please let me know right away if you find other programs that have conflicts with the new plotPost(). Greatly appreciated!

Mixture of Normal Distributions

In this post I show a simple illustration of a mixture of normal distributions. For the examples, we assume we have metric values that we suppose are generated by a mixture of two different normal distributions, which I'll call clusters. We don't know which datum came from each cluster. Our goal is to estimate the probability that each score came from each of the two clusters, and the means and SD of the normal distributions that describe the clusters.

The model specification (for JAGS): The assumes that the clusters have the same standard deviation, but different means.

model {
    # Likelihood:
    for( i in 1 : N ) {
      y[i] ~ dnorm( mu[i] , tau )
      mu[i] <- muOfClust[ clust[i] ]
      clust[i] ~ dcat( pClust[1:Nclust] )
    }
    # Prior:
    tau ~ dgamma( 0.01 , 0.01 )
    for ( clustIdx in 1: Nclust ) {
      muOfClust[clustIdx] ~ dnorm( 0 , 1.0E-10 )
    }
    pClust[1:Nclust] ~ ddirch( onesRepNclust )
}


The data specification:

# Generate random data from known parameter values:
set.seed(47405)
trueM1 = 100
N1 = 200
trueM2 = 145 # 145 for first example below; 130 for second example
N2 = 200
trueSD = 15
effsz = abs( trueM2 - trueM1 ) / trueSD
y1 = rnorm( N1 )
y1 = (y1-mean(y1))/sd(y1) * trueSD + trueM1
y2 = rnorm( N2 )
y2 = (y2-mean(y2))/sd(y2) * trueSD + trueM2
y = c( y1 , y2 )
N = length(y)

# Must have at least one data point with fixed assignment 
# to each cluster, otherwise some clusters will end up empty:
Nclust = 2
clust = rep(NA,N) 
clust[which.min(y)]=1 # smallest value assigned to cluster 1
clust[which.max(y)]=2 # highest value assigned to cluster 2 
dataList = list(
    y = y ,
    N = N ,
    Nclust = Nclust ,
    clust = clust ,
    onesRepNclust = rep(1,Nclust)
)

Results when mean of cluster 2 is 3 standard deviations away from mean of cluster 1: The posterior recovers the generating values fairly well.

Upper panel: Data with underlying normal generators.
Lower panel: For each datum, the posterior probability that it is assigned to cluster 2.

Marginal posterior on cluster means and SD.

Pairs plot of cluster means and SD.

Results when mean of cluster 2 is 2 standard deviations away from mean of cluster 1: There is lots of uncertainty. See captions for discussion.

Lower panel: Notice that the lowest and highest data values have fixed cluster assignments, but all the other data values have posterior probabilities of cluster assignment noticeably far from 0 or 1.

Notice the bimodal distribution of sigma (SD).

Notice in the in the right column that when sigma is small, around 15, then the cluster means are near their true generating values. But when sigma is large, then the cluster means get close together. Essentially, there is a bimodal posterior: Either there are two clusters, with smaller sigma and distinct means, or there is one cluster, with larger sigma and both cluster means set near the mean of the one cluster.

Beta distribution parameterized by mode instead of mean

In this post, I describe how it is easier to intuit the beta distribution in terms of its mode than its mean. This is especially handy when specifying a prior beta distribution. 

(In a previous post, I explained how it is easier to intuit the gamma distribution in terms of its mode instead of its mean.)

A problem with using the mean to describe a distribution is that for skewed distributions, the mean may be far from the mode, but the mode may be what we intuitively want as the "descriptive handle" on the distribution, and therefore the mean is not a good surrogate for the description of central tendency. Especially when we are specifying a prior distribution, we may want to express our intuition in terms of the mode of the prior instead of the mean.

For a beta distribution with shape parameters a and b, the mode is (a-1)/(a+b-2). Suppose we have a desired mode, and we want to determine the corresponding shape parameters. Here's the solution. First, we express the "certainty" of the estimate in terms of the equivalent prior sample size,

k=a+b, with k≥2. 

The certainty must be at least 2 because it essentially assumes that the prior contains at least one "head" and one "tail," which is to say that we know each outcome is at least possible. Then a little algebra reveals:

a = mode * (k-2) + 1

b = (1-mode) * (k-2) + 1

Here are a few examples:

 

The book expressed beta distributions in terms of mean and certainty instead of mode and certainty; cf. Eqn. 5.5, p. 83, where m denoted the mean and n denoted the certainty instead of k used here.

Improved Programs for Hierarchical Bayesian ANOVA

I've made three important changes in the programs for hierarchical Bayesian ANOVA.

First, I changed the hyperprior on the variance (standard deviation) parameters. I was never pleased with the "+.1" kludge that I used in the book, explained on p. 496: "There is one other trick in the BUGS model specification that is not in the hierarchical diagram of Figure 18.1. One line of the BUGS model specifies that the standard deviation of the group effects, denoted aSDunabs, comes from a t distribution: aSDunabs ~ dt(0,0.001,2). Another line takes the absolute value to “fold” the t distribution onto the nonnegative numbers: aSD <- abs(aSDunabs) + .1. But that line also mysteriously adds a small constant, namely 0.1. This constant keeps aSD from venturing extremely close to zero. The reason for keeping aSD away from zero is that shrinkage can become overwhelmingly strong when there are many groups with few data points per group. This becomes especially problematic in the next chapter when we consider interaction of factors." A problem with that kludge is that the aSD parameter can never be less than 0.1, which is unlikely to reflect a real prior belief. It can produce strangely truncated posterior distributions. Therefore I simply abandoned the folded-t prior (recommended by Gelman, 2006) and used a reasonable gamma instead. The gamma prior, for each SD parameter, has a mode at 0.1 and a standard deviation of 10, which seems to be an appropriate scaling when the data are standardized (as indeed they are in the programs). Here's a picture of this prior:

The neat thing about this prior is that it smoothly drops down to zero as the parameter value gets close to zero. (For how to specify a gamma prior with a desired mode and standard deviation, see this previous blog post.) The prior on the within-cell SD remains uniform, as in the original programs and recommended by Gelman (2006).

Second, I changed the plots of the variance parameters so that they are on the original data scale, not the standardized scale. This was achieved merely by multiplying by ySDorig.

Third, I changed how contrasts are specified. The original method was problematic because the contrasts were specified as vectors of contrast coefficients, which (a) lacked explicit meaning and (b) only made sense if the order of the levels of the factors was exactly as assumed by the contrast coefficients. Unfortunately, it turns out that different settings of R's "locale" can produce different orderings of the factor levels, rendering the contrast coefficients nonsensical! (Thanks to Damion Junk for pointing out this problem to me.) The new method uses logical indexing of named levels, so that the contrast specification is meaningful and independent of local ordering conventions. For example, for the mussel muscle data, the old contrast specification was
  contrastList = list( ...
    ORE1vORE2 = c(1,-1,0,0,0) ,
    ALAvORE = c(-1/2,-1/2,1,0,0) ,
    ... )
but the new specification is
  normalize = function( v ){ return( v / sum(v) ) }
  contrastList = list( ...
    ORE1vORE2 = (xnames=="OregonN")-(xnames=="OregonT") ,
    ALAvORE = (xnames=="Alaska")-normalize(xnames=="OregonN"|xnames=="OregonT") ,
    ...  )

Fourth, I improved the program for displaying posterior histograms, so that it now defaults to better breaks based on the HDI. Therefore it is best to use plotPost without a breaks argument unless the (new) default looks bad.

Where are the new programs? Get the updated files, ANOVAonewayJagsSTZ.R, ANOVAtwowayJagsSTZ.R, plotPost.R, and McDonaldSK1991data.txt, from the usual place (click the column labeled "Last Modified" to get the most recent listed first). ** Updated April 25, 2012. Also with the program PoissonExponentialJagsSTZ.R **

Negative Binomial Reparameterization

In a previous post, I showed that direct estimation of the p and r parameters in a negative binomial distribution could involve bad autocorrelation in the MCMC chains, and I suggested that there must be some standard reparameterization to solve the problem, and asked for a pointer. Dr. John Davey of the University of Edinburgh was good enough to point the way. The solution is indeed straight forward: In the direct estimation, the p and r parameters are given priors, while the mean m (and variance v) is derived from p and r. In the reparameterization, the m and r parameters are given priors, while the p (and variance v) is derived from m and r. Autocorrelation in the chains is greatly reduced. Here is an example.

The model specifications:

Parameterized by p and r:

model {
    for( i in 1 : N ) {
      y[i] ~ dnegbin( p , r )
    }
    p ~ dbeta(1.001,1.001)
    r ~ dgamma(0.01,0.01)
    m <- r*(1-p)/p
    v <- r*(1-p)/(p*p)
}

Parameterized by m and r:

model {
    for( i in 1 : N ) {
      y[i] ~ dnegbin( p , r )
    }
    p <- r/(r+m)
    r ~ dgamma(0.01,0.01)
    m ~ dgamma(0.01,0.01)
    v <- r*(1-p)/(p*p)
}

Results:

Parameterized by p and r:

Parameterized by m and r:

The posteriors are a bit different for the two parameterizations, because I used "generic" priors without any attempt to transform them to be equivalent.

Thanks to John Davey for this pointer!

Negative Binomial for Count Data

I have noticed that when estimating the parameters of a negative binomial distribution for describing count data, the MCMC chain can become extremely autocorrelated because the parameters are highly correlated. Question: There must be some standard re-parameterization, or other approach, to reducing this autocorrelation. Can someone point me to it?

[Update: See this follow-up post.]

Here is an example of what I mean. First, a histogram of the data, consisting of a 50 individual counts. (E.g., for each of 50 subjects, the number times they checked their e-mail in the last hour.) The histogram of data has posterior-credible negative binomial distributions superimposed.

Here is the JAGS model statement:

model {
    # Likelihood:
    for( i in 1 : N ) {
        y[i] ~ dnegbin( p , r )
    }
    m <- r*(1-p)/p
    # Prior:
    r ~ dgamma(gSh,gRa)
    p ~ dbeta(1.001,1.001)
}

Although the MCMC chain comes up with reasonable estimates in the long run, there is a lot of autocorrelation along the way:

It is clear that the reason for the autocorrelation is the strong correlation of the parameters:

As I said above, there must be some well-known way to address this issue. Can someone point me to it? Thanks.

Bayesian estimation supersedes the t test

[Updated here.]
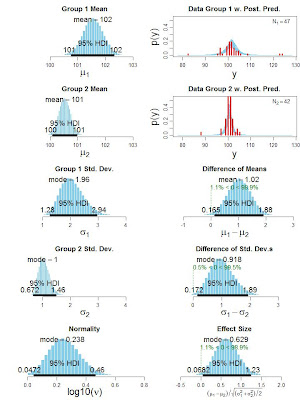
Bayesian estimation for two groups provides complete distributions of credible values for the effect size, group means and their difference, standard deviations and their difference, and the normality of the data. The method handles outliers. The decision rule can accept the null value (unlike traditional t tests) when certainty in the estimate is high (unlike Bayesian model comparison using Bayes factors). The method also yields precise estimates of statistical power for various research goals. The software and programs are free, and run on Macintosh, Linux, and Windows platforms. See this linked page for the paper and the software.

Search tag: BEST (for Bayesian estimation)

(A previous post announced an earlier version of this report and software.)