Extrasensory Perception (ESP): Bayesian estimation approach to meta-analysis

Bayesian analysis has recently attracted attention because of its application to data from experiments that investigate extrasensory perception (a.k.a. non-local perception, psi phenomena, etc.). There have been Bayesian analyses and re-analyses of data that were initially analyzed by NHST (see e.g., "Feeling the Future" by Bem (2011), a critique by Wagenmakers et al. (2011), a rejoinder by Bem, Utts & Johnson, and related discussion by Kruschke (2011). In their exchange, Wagenmakers et al. and Bem et al. emphasized Bayesian model comparison, not Bayesian parameter estimation, which are explained and contrasted by Kruschke (2011). In this blog post I show a Bayesian estimation approach to meta-analysis of ESP data.

The data. The specific motivation for this post started when my attention was attracted to a recent article,

Tressoldi, P. E. (2011). Extraordinary claims require extraordinary evidence: the case of non-local perception, a classical and Bayesian review of evidences. Frontiers in Psychology, 2(117), 1-5. doi: 10.3389/fpsyg.2011.00117

which, in turn, led me to the summary data in

Storm, L., Tressoldi, P. E., & Di Risio, L. (2010). Meta-Analysis of Free-Response Studies, 1992–2008: Assessing the Noise Reduction Model in Parapsychology. Psychological Bulletin, 136(4), 471-485. doi: 10.1037/a0019457

Storm et al. (2010) provide summary data from 67 experiments. In all of the experiments, data were in the form of dichotomous correct/wrong judgments out of a fixed pool of choices. In 63 of the 67 experiments, there were 4 choices, hence chance responding was 1/4. (The other experiments: For May (2007) chance was 1/3; for Roe & Flint (2007) chance was 1/8; for Storm (2003) chance was 1/5; and for Watt & Wiseman (2002) chance was 1/5. See Storm et al. (2010) for reference info.) Storm et al. (2010) computed summary data for each experiment by summing across trials and subjects, yielding a total correct out of total trials for each experiment. Storm et al. (2010) also divided the experiments into three types of procedure, or categories: Ganzfeld (C1), Non-Ganzfeld noise reduction (C2), and free response (C3).

The New Analysis. The 63 experiments that have chance performance at 1/4 are exactly the type of data that can be plugged into the hierarchical model in Figure 9.7 (p. 207) of the book, reproduced at right, using program BernBetaMuKappaBugs.R. Trial i in experiment j has response y_ji (1=correct, 0=wrong), as shown at the bottom of the diagram. The estimated underlying probability correct for experiment j is denoted θ_j. The underlying probabilities correct in the 63 experiments are described as coming from an overarching beta distribution that has mean μ and "certainty" or "tightness" κ. The model thereby estimates probability correct for individual experiments and, at the higher level, across experiments. In particular, the parameter μ indicates the underlying accuracy across experiments. We are primarily interested in the across-experiment level because we want to know what we can infer by combining information from many experiments. But the estimates at the individual-experiment level are also interesting, because they experience shrinkage from the simultaneous estimation of other experiment parameters in the hierarchical model. The constants in the top-level prior were set to be vague and non-committal; in particular A=1 and B=1 so that the beta prior on μ was uniform. The MCMC chains were burned-in and thinned so they were nicely converged with minimal autocorrelation. The MCMC sample contained 10,000 points.

Results. First I'll show results for each category, then combined across categories. For category C1 (Ganzfeld), here are histograms of the marginals on each parameter:

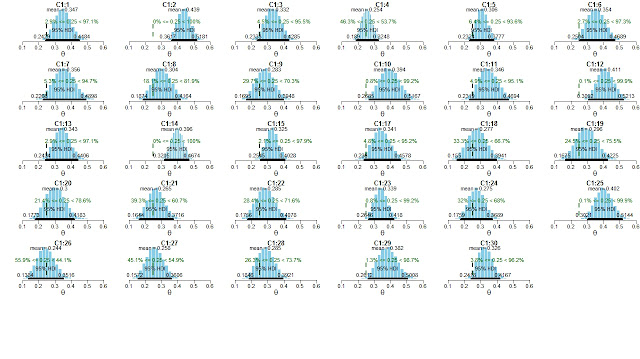Click image to view it enlarged, but click "back" in your browser to come back here!

The across-experiment μ (top left) is clearly above chance, with 100% of the posterior sample falling above 0.25. The 95% HDI goes from 0.288 to 0.366.

The estimates for the 29 individual experiments reflect shrinkage; for example, C1:25 has a mean posterior θ of 0.402, but in the data the proportion correct was 23/51 = 0.451. In other words, the estimate for the experiment has been shrunken toward the central tendency of all the groups. The estimates for the 29 individual experiments also reflect the sample sizes in each experiment; for example, C1:19 had only 17 trials, and its HDI is relatively wide, whereas C1:14 had 138 trials, and its HDI is relatively narrow. And, of course, experiments with smaller samples can experience more shrinkage than experiments with larger samples.

Results from category C2 are similar but less strong, and results from C3 do not exclude μ=0.25:

The results for C3 (above) are not as strong as they could be because the three experiments that were excluded (because they did not have chance at 1/4) all had results very different from chance! Thus, the results for C3 are artificially weaker than they should be, due to a selection bias.

The differences between μ₁, μ₂, and μ₃ are shown here:

Although μ₃ might be deemed to be different from the others, it is not a strong difference, and, as mentioned above, the magnitude of μ₃ was artificially reduced by excluding three experiments with high outcomes. Therefore it is worth considering the results when all 63 experiments are included together. Here are the results:

Using a Skeptical Prior: It is easy to incorporate skepticism into the prior. We can express our skepticism in terms of chance performance in a large number of fictitious previous experiments. For example, we might equate our skepticism with there having been 400 previous experiments with chance performance, so in the hyperprior we set A=100 and B=300. This hyperprior insists that μ falls close to 0.25, and only overwhelming evidence will shift the posterior away μ=0.25. A skeptic would also assert that all experiments have the same (chance) performance, not merely that they are at chance on average (with some above chance and others below chance). Hence a skeptical prior on κ would emphasize large values that force the θ_j to be nearly the same.

Bayesian estimation vs Bayesian model comparison. A general discussion of Bayesian estimation and Bayesian model comparison can be found in Kruschke (2011) and at other posts in this blog. In the present application, a major advantage of the estimation approach is that we have an explicit distribution on the parameter values. The analysis explicitly reveals our uncertainty about the underlying accuracy in each experiment and across experiments. The hierarchical structure also lets the estimate of accuracy in each experiment be informed by data from other experiments. On the other hand, Bayesian model comparison often provides only a Bayes factor, which tells us only about the relative credibility of the point null hypothesis and another specific non-null prior hypothesis, without telling us what the parameter values could be.

The Bayesian estimation approach is also very flexible. For example, data from individual subjects could be modeled as well. That is, instead of collapsing across all trials and subjects, every subject could have an estimated subject-accuracy parameter, and the subjects within an experiment are modeled by an experiment-level beta distribution that has mean θ_j, and the higher levels of the model are as already implemented here. Doing model comparisons with such a model can become unwieldy.

If our goal were to show that the null hypothesis is true, then Bayesian model comparison is uniquely qualified to express the point null hypothesis, but only in comparison to a selected alternative prior. And even if the Bayes factor in model comparison favors the point null, it provides no bounds on our uncertainty in the underlying accuracy. Only the estimation approach provides explicit bounds on the uncertainty of the underlying accuracies, even when those accuracies are near chance.

The file drawer problem. The file-drawer problem is the possibility that the data in the meta-analysis suffer from a selection bias: It could be that many other experiments have been conducted but have remained unpublished because the results were not "significant". Therefore the studies in the meta-analysis might be biased toward those that show significant results, and under-represent many non-significant findings. Unfortunately, this is a problem with biased sampling in the data, and the problem cannot be truly fixed by any analysis technique, Bayesian or otherwise. Storm et al. (2010) describe a couple methods that estimate how many unpublished null results would be needed to render the meta-analysis non-significant (in classical NHST). You can judge for yourself if those numbers are impressive or not. The file drawer problem is a design issue, not an analysis issue. One way to address the file drawer problem is by establishing the procedural convention that all experiments must be publicly registered before the data are collected. This procedure is an attempt to prevent data from being selectively filtered out of public view. Of course, it could be that people in the experiments would be able to sense that the experiment had been pre-registered (through non-local perception), which would interfere with their ability to exhibit further ESP in the experiment itself.

So, does ESP exist? The Bayesian estimation technique says this: Given the data (which might be biased by the file drawer problem), and non-committal priors (which do not reflect a skeptical stance toward ESP), the underlying probability correct is almost certainly greater than chance. Moreover, the estimation provides explicit bounds on the uncertainty for each experiment and across experiments. For skeptical priors, the conclusion might be different, depending on the degree of skepticism, but it's easy to find out. No analysis can solve the file-drawer problem, which can only be truly addressed by experiment design procedures, such as publicly registering an experiment before the data are collected (assuming that the procedure does not alter the data).